一位数学家解释说,如何使冠状病毒的曲线变平

进入澳大利亚的人现在必须自隔离14天 - 总理斯科特莫里森周末宣布的一系列措施之一,旨在放缓冠状病毒的蔓延,缓解医院病床的压力。
这种减缓病毒传播的一般概念被流行病学家称为“使曲线变平”。流行病学家是研究疾病在不同人群中发生的频率及其原因的专家。这个术语已经成为社交媒体普及因为公众被鼓励实行“社会距离”。
但是社交距离是如何使曲线变平的呢?我们可以用数学家所说的“指数增长”来解释。
指数级增长
在疫情的早期阶段,当大多数人都易受感染时,数学家可以模拟一种疾病从人的蔓延到人类,就像随机的“分支过程”。
如果一个受感染者平均感染其他两种人,那么受感染者的人数都会增加每一代。这种复合称为指数级增长。
当然,一个被感染的人不是确实会传染给其他人。有许多因素影响感染的可能性。在大流行中,增长率取决于一个人可以感染的平均人数,以及这些人自己被感染所需要的时间。
研究表明,全球新冠肺炎确诊病例呈指数级增长,增加了一倍大约每六天一次
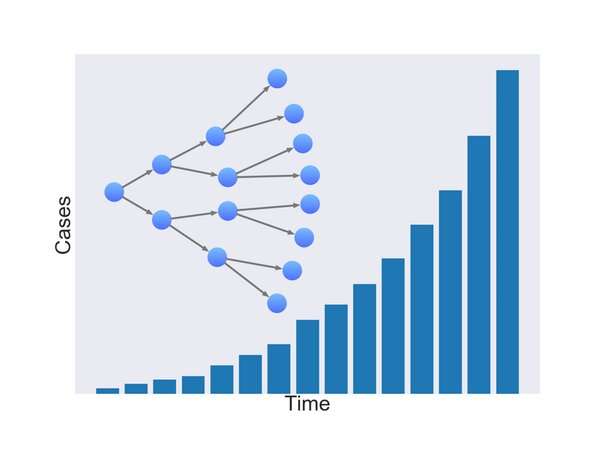
当病毒首次出现在武汉时,或者当它到达意大利或伊朗时,指数增长模型与现实非常吻合。
但一旦有大量的人被感染,这就不是一个好的模式。这是因为感染者接触易感人群的机会减少了,仅仅是因为周围易感人群减少了,越来越多的人已经恢复并发展了某种程度的免疫力。
最终,感染者接触敏感人的人的机会变得足够低,以至于感染率降低,导致较少的病例和最终,病毒蔓延的结束。
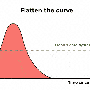
平曲线
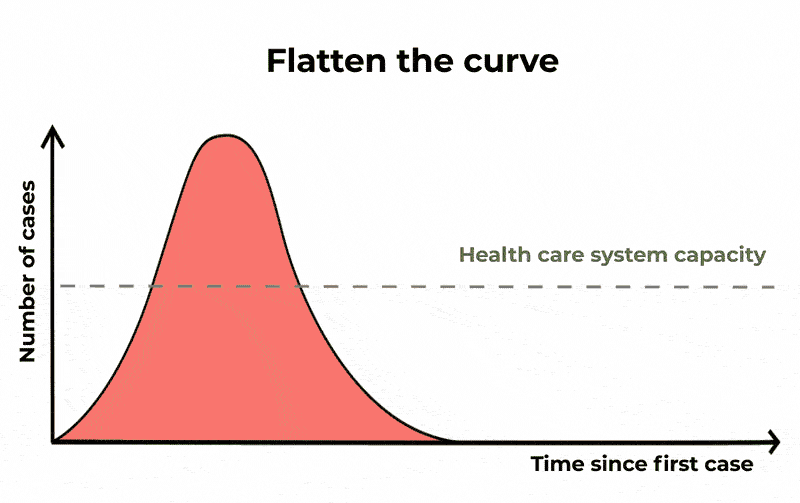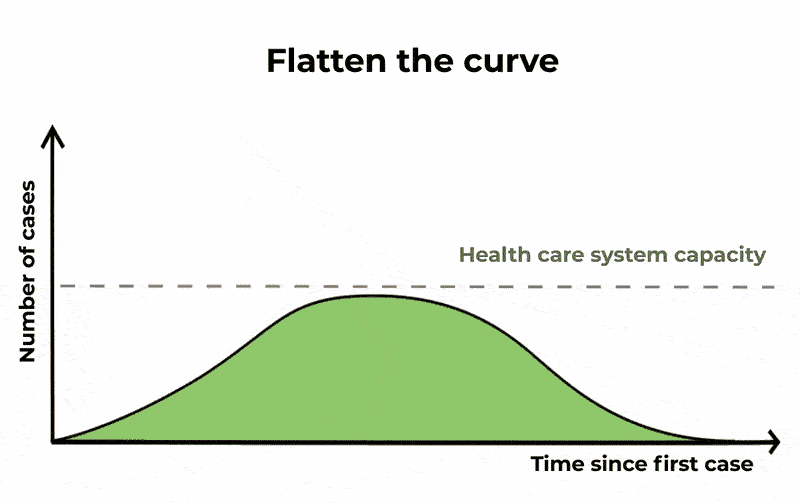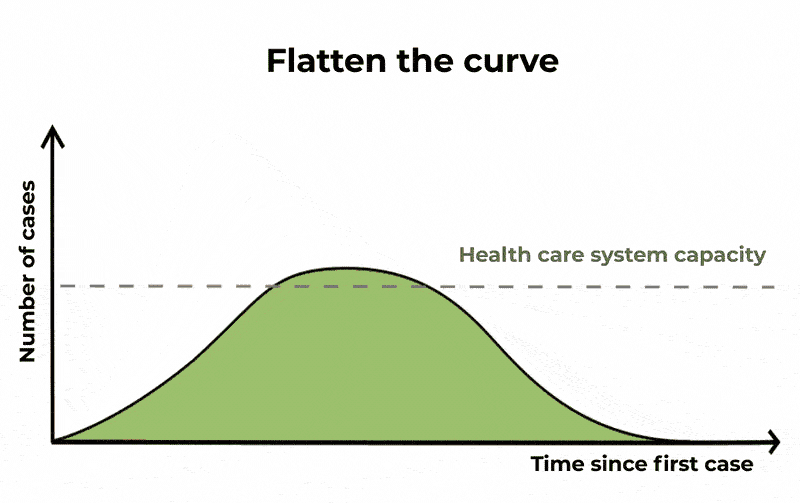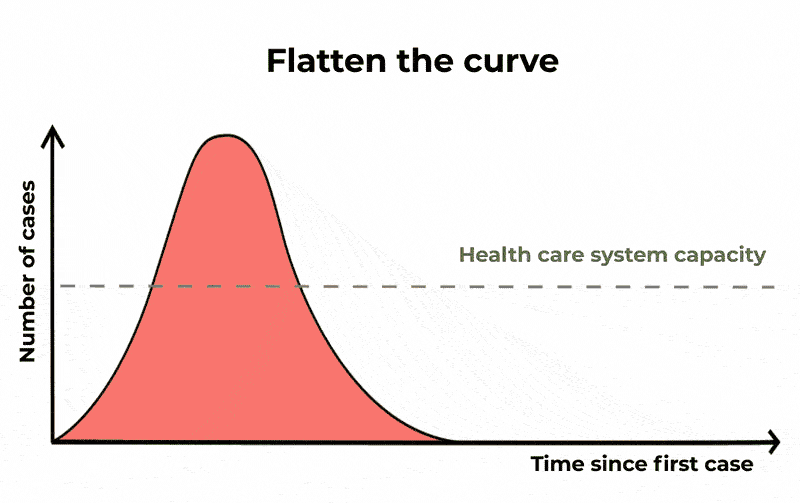
世界各地的卫生当局一直无法完全防止Covid-19的传播。如果案件每六天每六天,那么医院和重症监护单位(ICU)尤其会很快被淹没,让患者没有必要的护理。
但是,增长率可以通过减少单个案件引起的平均案件数量来减缓。
这样一来,可能会有相同数量的人受到感染,疫情将持续更长时间,但严重病例的数量将会分散。这意味着,如果你绘制一段时间内病例数量的曲线图,上升和下降的曲线更长,但峰值更低。通过这种方式“拉平曲线”,icu将不太可能耗尽容量。
由于目前没有针对COVID-19的疫苗或特定药物,我们减少传播的唯一途径是通过良好的卫生、隔离疑似病例,以及通过取消大型活动和关闭学校等社交距离措施。
避免“超级传播者”
当然,这种情况并不像简单的分支过程那样简单。有些人比其他人互动更多,可能会接触到许多不同的群体。
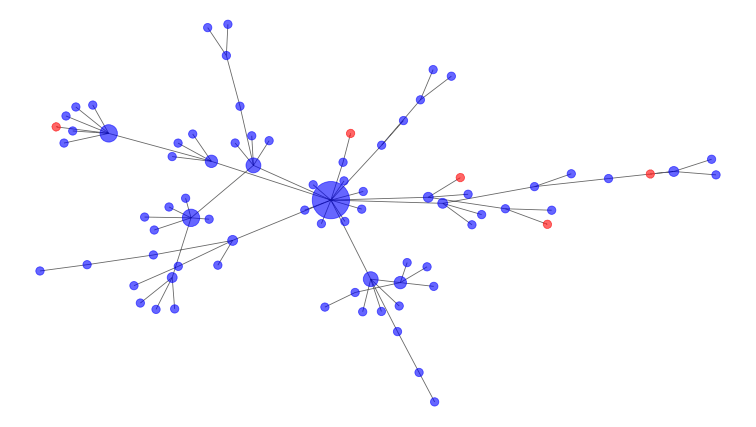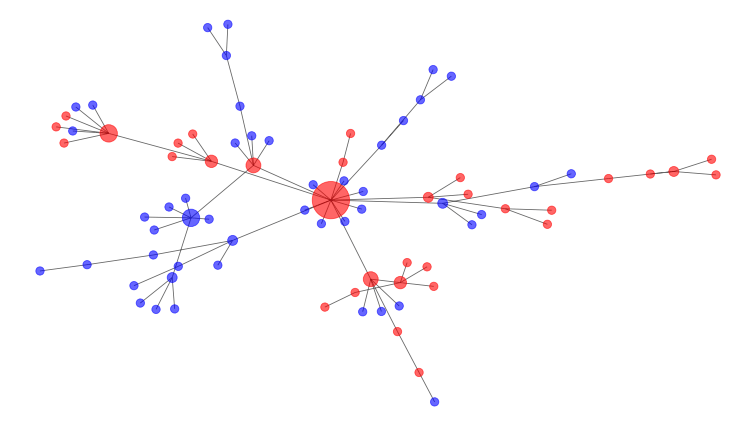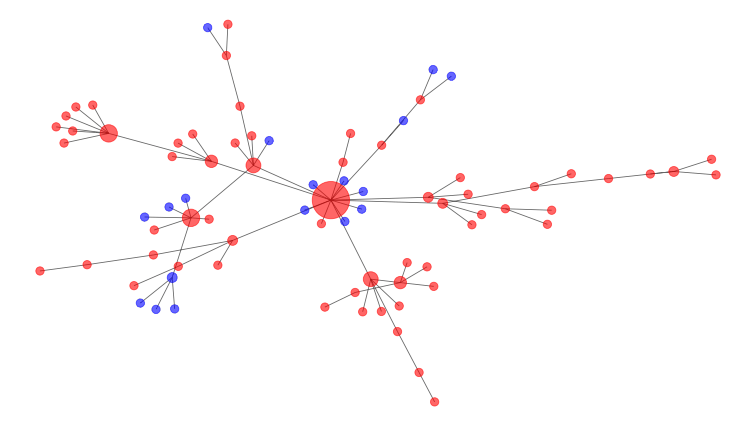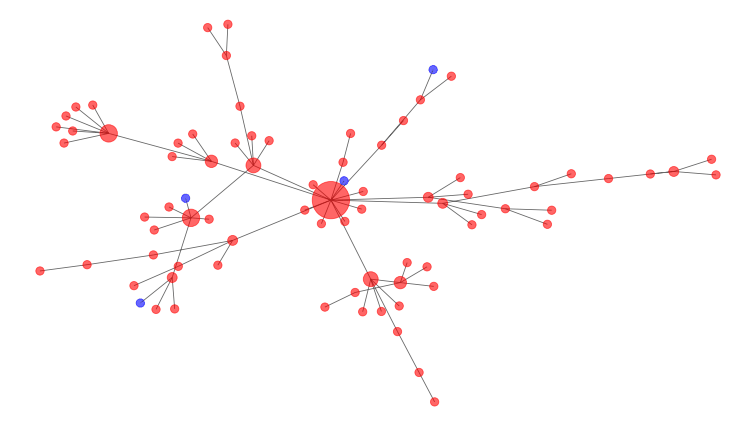
数学家将这些连接模拟为社交网络,例如下面的联系。受感染的人是红色节点,易感人是蓝色的。图中间的大节点是一个超级吊具,一个与众不同的人,因此有更多的潜力来传播疾病。
干预措施有助于删除节点和中断连接。
在上图中,大型高度连接的中央节点是最佳删除以中断连接的节点。这就是为什么在Covid-19爆发期间避免大型公共集会是一个好主意。
对社交距离的数学模拟显示,打破网络有助于使感染曲线变平。
数学是如何帮助的
需要多少社会偏差来压平曲线,以阻止医院不堪重负?是否足以检测与确认案件联系的人?我们是否需要广泛地关闭活动,学校和工作场所?
这些问题的答案需要数学建模。
我们仍处于新冠肺炎疫情的早期阶段,这种病毒的特征存在很大的不确定性。为了准确预测COVID-19的增长,需要确定传播的基本动态。
这些因素包括:
- 平均每个人会感染多少人?(“繁殖数量而根据世界卫生组织(who)的数据,这是目前的情况1.4-2.5人之间)
- 多久才会出现症状?("潜伏期",估计为5.1天)
- 在出现症状之前发生传播的比例是多少?
由于这些数据在未来几个月内收集并集成到模型中,我们将更好地倾向于对Covid-19的过程提供准确的预测。
在那之前,最好是谨慎行事,迅速采取行动减缓传播,而不是冒病例激增的风险,给我们的卫生系统带来压力。








用户评论